Twenty-five years too late to assist Ross get his new sofa into his residence in “Friends,” a mathematician has lastly solved the pesky “couch downside.”
The math downside delineates the largest-size couch that may match round a nook of a given width — precisely the issue confronted by the characters in an episode of “Friends” that aired in 1999. Ross’ pleas of “Pivot!” may have been averted, it seems, if he’d solely thought of a Gerver’s couch with 18 curve sections and a most space of two.2195 models. (Okay, so possibly it would not have been that useful.)
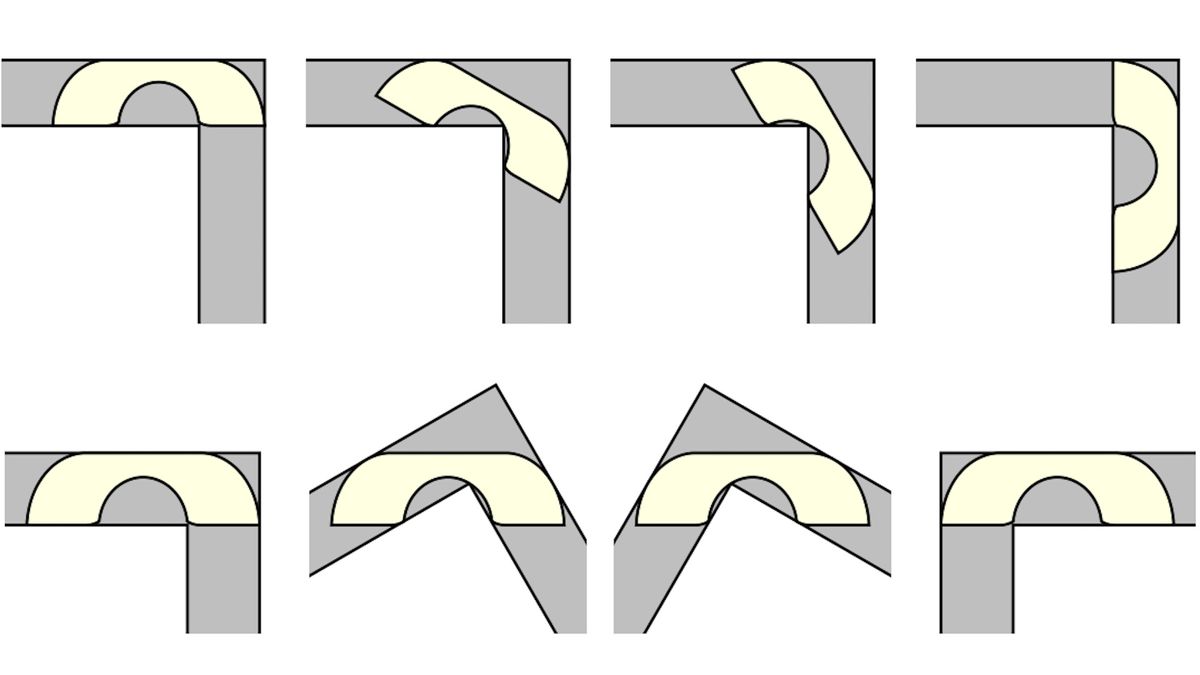
The answer to the couch downside is a primary for arithmetic. The downside was posited by Austrian-Canadian mathematician Leo Moser in 1966. Moser requested for the biggest doable space of a single form in a single aircraft that would transfer round a right-angled nook of a hallway with a unit width of 1. While this might sound easy, the mathematics is kind of sophisticated, as the issue includes each space maximization and motion of the form.
Now, Jineon Baek, a postdoctoral researcher in arithmetic at Yonsei University in South Korea, has arrived at a solution. Baek posted his answer on Dec. 2 on the preprint web site ArXiv. In simply over 100 pages of mathematical proofs, Baek discovered that for a hallway with a width of 1 unit, the imaginary couch’s most space will be 2.2195 models — narrowing the reply down with precision from the beforehand recognized vary of between 2.2195 and a pair of.37 models. The proof has not but been revealed in a peer-reviewed journal and can have to be labored by way of by different mathematicians to find out that it’s, certainly, optimum.
Related: High college college students who got here up with ‘unattainable’ proof of Pythagorean theorem uncover 9 extra options to the issue
The “Gerver” of Gerver’s couch is mathematician Joseph Gerver, an emeritus professor at Rutgers University who posited the decrease sure of two.2195 in 1992. But there had been debate over whether or not the couch could possibly be bigger, with a staff in 2018 utilizing a computer-assisted proof to recommend that 2.37 was truly the higher sure.
Gerver’s couch is a broad U-shaped sofa with a curved “seat” that may squeeze across the nook with out getting hung up. The query was whether or not this painstakingly designed couch — manufactured from 18 separate curves put collectively — was actually the biggest, most optimum form that would make the flip. Baek labored by way of the geometry of the form and its motion and located that Gerver’s answer was, the truth is, appropriate.
The proof created a ripple of curiosity on social media.
“This is the optimum couch,” person @morallawwithin wrote on the social platform X on Dec. 6, posting an image of the somewhat wide-armed couch form. “You could not prefer it, however that is what peak optimization appears like.”