• Physics 17, 182
A brand new principle associated to the second regulation of thermodynamics describes the movement of energetic organic programs starting from migrating cells to touring birds.
In 1944, Erwin Schrödinger printed the guide What is life? [1]. Therein, he reasoned in regards to the origin of residing programs by utilizing strategies of statistical physics. He argued that organisms type ordered states removed from thermal equilibrium by minimizing their very own dysfunction. In bodily phrases, dysfunction corresponds to constructive entropy. Schrödinger thus concluded: “What an organism feeds upon is unfavourable entropy […] releasing itself from all of the entropy it can not assist producing whereas alive.” This assertion poses the query of whether or not the second regulation of thermodynamics is legitimate for residing programs. Now Benjamin Sorkin at Tel Aviv University, Israel, and colleagues have thought of the issue of entropy manufacturing in residing programs by placing ahead a generalization of the second regulation [2]. Using an information-theoretic framework, they present that their principle can be utilized to derive necessary thermodynamic portions and relations for residing programs.
Sorkin and colleagues constructed upon ideas developed over the previous few many years. In the early Nineties, scientists pioneered the research of fluctuation relations, which generalize the second regulation of thermodynamics to single-particle programs removed from thermal equilibrium [3]. In parallel, different researchers laid the foundations of stochastic thermodynamics, which takes elementary thermodynamic ideas (e.g., warmth, work, and entropy) developed for many-particle programs and applies them to stochastic single-particle dynamics [4]. This framework reproduces an entire hierarchy of beforehand derived fluctuation relations, together with the primary and second legal guidelines of thermodynamics for a randomly transferring, or Brownian, particle in a fluid [5].
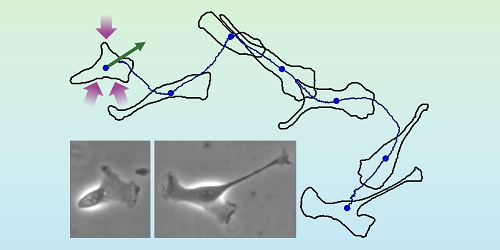
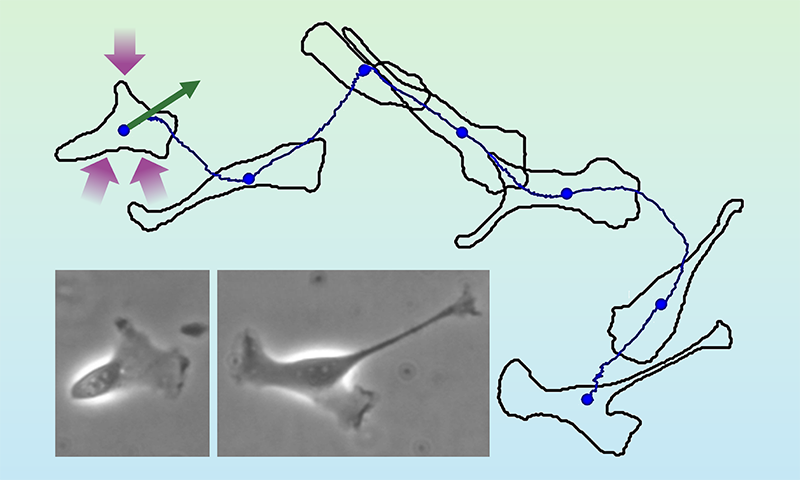
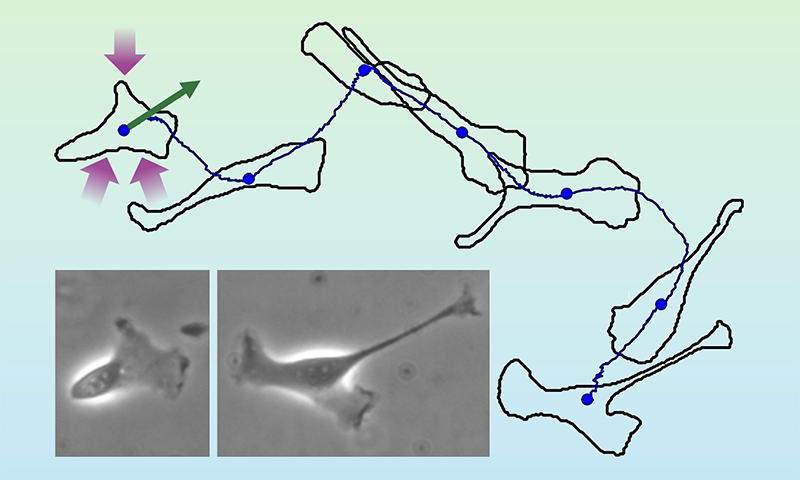
In the previous decade, fluctuation relations have been used to explain organic dynamics by linking stochastic thermodynamics with the rising area of energetic matter [6]. Examples of active-matter programs vary from migrating organic cells to flocks of birds to transferring crowds of individuals [7]. Active movement is self-driven, in stark distinction to the passive dynamics of a Brownian particle. Think of a crawling cell, which propels itself utilizing vitality taken up from its surroundings (Fig. 1). The cell’s path seems to be random, akin to the trajectory of a Brownian particle in a fluid. But whereas such a particle is passively pushed by collisions with surrounding fluid molecules, the cell strikes actively by itself.
The dynamics of a Brownian particle is characterised by a stability between the particle’s fluctuations in motion and its dissipative interplay with its surroundings. Such stability is expressed when it comes to the particle’s diffusion coefficient, its mobility, and the temperature of the encircling fluid. This so-called Einstein relation is an instance of a fluctuation–dissipation relation that holds for unusual classical fluids [3–5]. However, in additional complicated programs equivalent to polymer gels, the Einstein relation is damaged, resulting in violations of standard fluctuation relations [8]. In energetic matter, the Einstein relation is often additionally damaged, reflecting the particular uptake of vitality and conversion into self-propelled movement [7].
Sorkin and colleagues began from a so-called overdamped Langevin equation, which can be utilized to mannequin the dynamics of programs with out assuming the Einstein relation. Such modeling contains examples of energetic matter and passive Brownian particles as particular circumstances. By making use of stochastic thermodynamics [4, 5], the workforce rederived the primary and second legal guidelines of thermodynamics by assuming the existence of an unusual thermodynamic temperature, as within the Einstein relation.
The researchers then thought of a vital amount in stochastic thermodynamics generally known as informatic entropy manufacturing, which measures the breaking of time-reversal symmetry on the extent of microscopic trajectories. Without assuming the Einstein relation and its corresponding thermodynamic temperature, however by imposing three particular bodily circumstances, Sorkin and colleagues derived an equation for what they name a generalized nonequilibrium temperature. Using this equation, one obtains a second regulation with out the Einstein relation. If one then assumes this relation, the researchers’ generalized temperature boils right down to the unusual thermodynamic temperature, and their principle recovers corresponding outcomes for standard stochastic thermodynamics.
An necessary consequence of the brand new principle is that, with out the Einstein relation and related thermodynamic temperature, standard fluctuation relations are recovered solely on an summary, information-theoretic degree and never for thermodynamic portions—in step with earlier work [8]. Assuming a generalized temperature, one can derive helpful thermodynamic relations such because the Clausius inequality, a generalized “Carnot effectivity,” and bounds between two key portions—the extractable work and the free-energy change. Sorkin and colleagues recommend that their idea of a generalized temperature may very well be verified by making use of their principle to sure experimental programs through which the Einstein relation is damaged.
Achieving the derivation of a brand new type of the second regulation that applies to residing programs is sort of a giant declare. Given that the speculation doesn’t require the Einstein relation, one may name it a second regulation of athermal dynamics, the place right here “athermal” denotes the nonthermodynamic energetic organic forces that trigger deviations from classical thermodynamics [5]. Notably, the speculation assumes that the dynamics is each overdamped and Markovian—that’s, unbiased of the system’s historical past. However, the overdamped approximation, which neglects acceleration and inertia, can fail when fluctuations rely upon place, equivalent to for temperature gradients [9]. Moreover, many energetic organic programs—equivalent to migrating cells—exhibit non-Markovian anomalous diffusion [10]. Along these strains, violations of fluctuation–dissipation relations which might be extra common than the Einstein relation can come into play [8].
These issues name for additional generalizations of the brand new principle, as envisioned by Schrödinger [1]: “Living matter, whereas not eluding the ‘legal guidelines of physics’ as established updated, is more likely to contain ‘different legal guidelines of physics’ hitherto unknown, which, nonetheless, as soon as they’ve been revealed, will type simply as integral part of this science as the previous.”
Acknowledgments
Rainer Klages acknowledges Lennart Dabelow of the Queen Mary University of London for useful feedback on the article.
References
- E. Schrödinger, What is life? (Cambridge University Press, Cambridge, 2012)[Amazon][WorldCat].
- B. Sorkin et al., “Second regulation of thermodynamics with out Einstein relation,” Phys. Rev. Lett. 133, 267101 (2024).
- D. J. Evans et al., Fundamentals of Classical Statistical Thermodynamics: Dissipation, Relaxation, and Fluctuation Theorems: (Wiley, Weinheim, 2016)[Amazon][WorldCat].
- Ok. Sekimoto, Stochastic Energetics, Lecture Notes in Physics Vol. 799 (Springer, Berlin, 2010)[Amazon][WorldCat].
- U. Seifert, “Stochastic thermodynamics, fluctuation theorems and molecular machines,” Rep. Prog. Phys. 75, 126001 (2012).
- L. Dabelow et al., “Irreversibility in energetic matter programs: Fluctuation theorem and mutual data,” Phys. Rev. X 9, 021009 (2019).
- S. Ramaswamy, “The mechanics and statistics of energetic matter,” Annu. Rev. Condens. Matter Phys. 1, 323 (2010).
- S. M. J. Khadem et al., “Stochastic thermodynamics of fractional Brownian movement,” Phys. Rev. Res. 4, 043186 (2022).
- A. Celani et al., “Anomalous thermodynamics on the microscale,” Phys. Rev. Lett. 109, 260603 (2012).
- P. Dieterich et al., “Anomalous dynamics of cell migration,” Proc. Natl. Acad. Sci. U.S.A. 105, 459 (2008).