In the world of arithmetic, two issues all the time maintain true: firstly, a number of the most cussed and complicated issues typically have surprisingly real-world functions; and secondly, for individuals who spend all their time really in that actual world, these issues can appear… nicely, fairly foolish.
Take, for instance, the “couch drawback”: a conundrum that has each stumped mathematicians for many years, and in addition been “solved” by nearly anyone who’s ever moved home of their life. It’s a query of learn how to transfer a curved couch round a 90-degree nook – sure, similar to in that one episode of Friends you’re all now quoting.
The math of shifting
Technically, the couch drawback is that this: What is the area of largest space which might be moved round a right-angled nook in a hall of width one? It was first formally acknowledged in 1966 by the Austrian-Canadian mathematician Leo Moser – although it had been a subject of dialog across the mathematical water coolers for a few years earlier than that – and till now, by no means conclusively solved.
Now, you’ll discover that there’s no point out of the eponymous sofa on this formulation, and certainly the primary piece of “furnishings” instructed as an answer was really a “piano”. Nevertheless, the “couch” terminology quickly took off, largely as a result of – nicely, take a look at it:
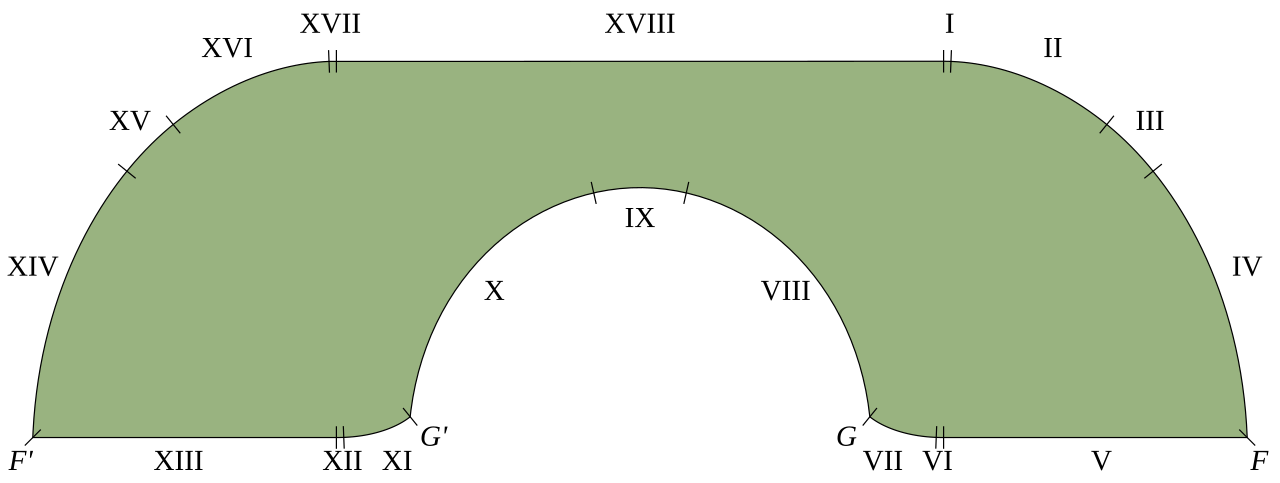
The Gerver couch, exhibiting every of the 18 segments making up its boundary.
It was the willpower of a decrease certain that gave rise to the enduring couch form: in a 1968 treatise named, we child you not, On the enfeeblement of mathematical expertise by ‘Modern Mathematics’ and by comparable comfortable mental trash in colleges and universities, John Hammersley confirmed with some comparatively easy calculus that this form gave an space of (π/2) + (2/π) – roughly 2.2074.
In reality, he went additional. In the identical paper, he proved that an higher certain on the realm was given by 2√2 – roughly 2.8284. It had solely been a few years, however the couch drawback was already on its approach to an answer: the precise determine hadn’t been nailed down but, however mathematicians knew it needed to be between these two values. Surely it wouldn’t take rather more work to seek out the true reply?
Fast ahead 25 years, although, and Hammersley’s bounds had been nonetheless the very best we had. That was, till Rutgers mathematician Joseph Gerver stepped as much as the plate, providing a settee constructed from 18 analytically clean linked curve sections. The “Gerver couch”, because it grew to become recognized, elevated the decrease certain to 2.2195.
It can be one other quarter-century once more earlier than the vary of attainable options can be pared down even additional: in 2018, mathematicians Yoav Kallus and Dan Romik used a computer-assisted proof to shave the higher certain all the way down to 2.37.
It was an enormous enchancment on Hammersley’s authentic bounds – however that actual answer was nonetheless evading seize.
Baek within the sport
It would have been across the similar time as Kallus and Romik had been engaged on their answer that Jineon Baek, a postdoctoral researcher at Yonsei University in Seoul, Korea, first began eager about the couch drawback. Now, seven years later, he reckons he’s cracked it in a proof that has but to be peer-reviewed.
“I devoted a variety of time to this, with none publication to this point,” he advised New Scientist. “The indisputable fact that now I can say to the world that I dedicated one thing precious to this drawback is validating.”
For a query so simply acknowledged and imagined, Baek’s proof was no small enterprise. Spanning greater than 100 pages, it does excess of merely brute pressure the issue or constantly shave off ever-smaller slices of space. Rather, it’s, Romik advised New Scientist, a “fantastic growth”.
“I do know I may by no means have performed this,” Romik stated. “I don’t have a sense of remorse, or like, how may I miss this, as a result of it’s clear it’s simply not the type of pondering that I feel I might have been in a position to. [Baek] was simply coming at it from a totally completely different course.”
Without stepping into the nitty-gritty, the proof goes like this: first, Baek stated that the optimum couch, no matter it turned out to be, needed to have three particular properties – it needed to be monotone, balanced, and have a rotation angle π/2. Again, these are fairly technical to outline, however basically it boils all the way down to this: the “couch” we’ve been utilizing to this point is just about the proper form already.
Secondly, Baek set about proving a situation on how this couch would transfer across the nook – a small factor, however essential for finishing the ultimate step: defining the higher certain for the realm of this couch, after which exhibiting that it was equal to Gerver’s decrease certain.
That’s proper: after 32 years, it seems Gerver was proper all alongside.
“I’m in fact very completely happy about all of this,” Gerver advised New Scientist. “I’m 75 years previous, and Baek can’t be greater than 30. He has much more power, stamina and surviving mind cells than I do, and I’m glad that he picked up the baton. I’m additionally very completely happy that I lived lengthy sufficient to see him end what I began.”
Put your toes up
So, is the couch drawback now full? Well, technically, it stays to be seen. As with all mathematical proofs, it must be peer-reviewed for accuracy – a course of that Baek is quietly longing for.
“I can’t say that I’m assured 100 per cent, as a result of we’re people, we make errors,” he advised New Scientist. “But nonetheless, I did my finest to be as assured as I can.”
But in case your hopes of fixing the couch drawback your self have been dashed by this information, take coronary heart: since Baek outlined his couch so strictly, you possibly can all the time select a distinct form on your personal.
It won’t make fairly pretty much as good a settee on your front room in fact, however there’s actually nothing stopping you from going… Baek to the drafting board, you would possibly say.
The proof might be discovered on the ArXiv preprint server.




